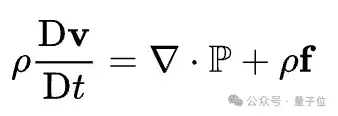- 周六 6月 21, 2025 9:16 am
#9423
罕见的陶哲轩(极长)访谈:数学、AI和给年轻人的建议
陶哲轩罕见接受了一次长长长长访谈,把他关于数学、AI、教育和人类智慧的最新认知,都对外分享了。
作为菲尔兹奖得主,陶哲轩一直被认为是当世最伟大的数学家之一,而这次在与MIT技术背景的播客大神Lex Fridman的对话,也是他近年来首次接受超3小时的非学术机构访谈,内容覆盖数学前沿、AI形式化验证、科研方法论等多个硬核议题。
陶哲轩罕见长长长长长访谈:数学、AI和给年轻人的建议

不仅谈论分享了数学和物理相关的专业性观点,还结合当下AI技术迅速发展的背景,作出了很多像基础教育和AI应用的大众话题思考……
陶哲轩金句频出,比如:
AI和菲尔兹奖的距离,只差一个研究生了。
复数意义上的人类共同体将创造出最顶尖的超级智能体,比单个数学家更有可能实现数学领域的突破。
数学的关键在于不仅是找到一个有效的技术路径,而是在几十种可能适用的方法中排除错误答案。
科学通常是三者之间的相互作用:现实世界、我们对现实世界的观察,以及我们认为世界如何运作的模型。
在理解和看待世界的方式上,数学从公理出发关注模型,物理由结论驱动注重收集结果。
在AI的协助下,数学在未来将会有更多的实验,而不仅仅是理论。
数学之美在于你可以随心所欲地改变规则,这是其它任何领域都无法做到的一点。
解决困难问题就像香港动作片,逐个击破,方得大成。
……
陶哲轩认为,AI正在重塑人类科学范式,数学和物理的终极问题上,AI将成为人类探索这些范式的重要伙伴,但无法取代人类的直觉与创造力。
而关于数学,他也深入浅出地谈论了以下世界级数学难题——
Kakeya猜想
纳维-斯托克斯正则性问题
塞迈雷迪定理
万物理论
广义相对论
庞加莱猜想
孪生素数猜想
克拉兹猜想
黎曼假设
费马大定理
嗯,是的,这就是一次高智力、高密度和高强度的三高对话,如果你也做好了“大脑尖叫”的准备,一起来看看我们整理过的访谈全文吧~~
https://www.qbitai.com/2025/06/299860.html
陶哲轩罕见接受了一次长长长长访谈,把他关于数学、AI、教育和人类智慧的最新认知,都对外分享了。
作为菲尔兹奖得主,陶哲轩一直被认为是当世最伟大的数学家之一,而这次在与MIT技术背景的播客大神Lex Fridman的对话,也是他近年来首次接受超3小时的非学术机构访谈,内容覆盖数学前沿、AI形式化验证、科研方法论等多个硬核议题。
陶哲轩罕见长长长长长访谈:数学、AI和给年轻人的建议

不仅谈论分享了数学和物理相关的专业性观点,还结合当下AI技术迅速发展的背景,作出了很多像基础教育和AI应用的大众话题思考……
陶哲轩金句频出,比如:
AI和菲尔兹奖的距离,只差一个研究生了。
复数意义上的人类共同体将创造出最顶尖的超级智能体,比单个数学家更有可能实现数学领域的突破。
数学的关键在于不仅是找到一个有效的技术路径,而是在几十种可能适用的方法中排除错误答案。
科学通常是三者之间的相互作用:现实世界、我们对现实世界的观察,以及我们认为世界如何运作的模型。
在理解和看待世界的方式上,数学从公理出发关注模型,物理由结论驱动注重收集结果。
在AI的协助下,数学在未来将会有更多的实验,而不仅仅是理论。
数学之美在于你可以随心所欲地改变规则,这是其它任何领域都无法做到的一点。
解决困难问题就像香港动作片,逐个击破,方得大成。
……
陶哲轩认为,AI正在重塑人类科学范式,数学和物理的终极问题上,AI将成为人类探索这些范式的重要伙伴,但无法取代人类的直觉与创造力。
而关于数学,他也深入浅出地谈论了以下世界级数学难题——
Kakeya猜想
纳维-斯托克斯正则性问题
塞迈雷迪定理
万物理论
广义相对论
庞加莱猜想
孪生素数猜想
克拉兹猜想
黎曼假设
费马大定理
嗯,是的,这就是一次高智力、高密度和高强度的三高对话,如果你也做好了“大脑尖叫”的准备,一起来看看我们整理过的访谈全文吧~~
https://www.qbitai.com/2025/06/299860.html