下面的这项工作很不错。提几点看法。作为一个数学研究结果,这是一项重要的工作。数学大厦是靠许多这样扎实的研究捡起来的。但这类的工作不宜作为数学人生的主要课题,那个格局要比这大多了。人生数学选题要选能够左右一大片数学方向的未知问题,研究它能开创新的领域方法和新的问题。
觉得下面这篇文章的解决方案太过细,这表明没有能抓到问题的实质。左右大局的研究一定是主线脉络推理清晰有力简洁,丝丝入扣的层次引人入胜渐次一路向着光明、美、高潮前行。没能抓住要领,证明就很繁琐甚至要有计算机加入(这靠不住)。原因还是结构没有弄得很清楚没抓住要领。但这未必完全是坏事。把这个结构和要领找出来这就是个大成就了。数学研究的本质本来就是对复杂的事物,通过研究它的结构,找到要点后,人们能够这个事物有个
简单的看法。如果这个看法太过复杂,就有违数学研究的本质。复杂的解觉方案可能只是原问题的转移,一个等价的新说法而已。
觉得华人数学家的很多人非常聪明能干,但开创性不够,格局小,急功近利老在想在什么地方“捡个漏”“补个漏”“补个缺”“吃个快餐”。根本原因可能是有些人觉得自己有一定的数学能力就可以用此能力“科举”谋取名利(升官发财、得到漂亮女人的爱睡她或睡很多女人、光宗耀祖),做数学不是为了搞清结构追求真理达到真理。很多美国欧洲学者做数学就真的是在全力以赴追求真理的。他们不奢求不放弃不妒忌,他们有的是永恒的数学。所幸的华人中也确实有少数数学家也进入了此状态和格局。也确实有(目前暂时还不为人知的低调)华人数学家也取得了了不起的大成果,是数学核心领域里的 0-1 的重大原创,关闭了一扇历史大门(解决了一个很长历史的大猜想)同时打开了几个新的通道(几个新的研究领域)。这个会震。
-------------------------

新智元报道
编辑:KingHZ
【新智元导读】3位华人数学家,终结了65年的代数拓扑中的著名问题!证明中105种假设路径中,计算程序成功排除了其中101种可能性,完成了计算上的壮举!
3位华人数学家,终结了65年的著名数学问题!
这个问题涉及的是有框流形(framed manifolds)。

二维有框流形的例子
大概10年前,3位数学家Michael Hill,Michael Hopkins和Doug Ravenel证明仅在维度2、6、14、30、62存在一种特殊的流形:Kervaire不变量等于1的光滑有框流形。
而126维空间,也很有可能存在这样的流形,但没有被证明。
而在去年,复旦大学的林伟南、王国祯以及UCLA的徐宙利这3位北大校友,证明了126维度空间中这种流形的确存在。
这个Kervaire不变量问题,困扰了数学家65年,终于被破解!
论文链接:
https://arxiv.org/abs/2412.10879

这项研究连接了两种研究这些形状的方法。
一种是拓扑学(topology),它关注的是形状的连接方式——即在不撕裂的前提下对形状进行拉伸、扭曲时,哪些性质保持不变。
另一种是微分拓扑(differential topology),它研究的是足够「平滑」的形状,从而可以使用微积分中的概念,比如切线和导数来分析这些形状的结构。
但这一次,不止是数学,计算机编程也扮演着重要角色。
为了给北京大学献上126周年的生日祝福,在2024年北大校庆期间,三位北大数学系校友林伟南(2011级)、王国祯(2004级)、徐宙利(2004级),在北京数学杂志(Peking Mathematical Journal)会议上公布了Kervaire不变量问题的彻底解决。
维度的个性
不同维度的空间,有着截然不同的「个性」。
比如说,只有三维空间中存在纽结(knots)——在更高维度中,即便紧紧抓住绳子的两端,也总能将一个打结的绳子解开。
普通人难以理解其中的乐趣和奥秘,但至少数学家能证明的确如此。
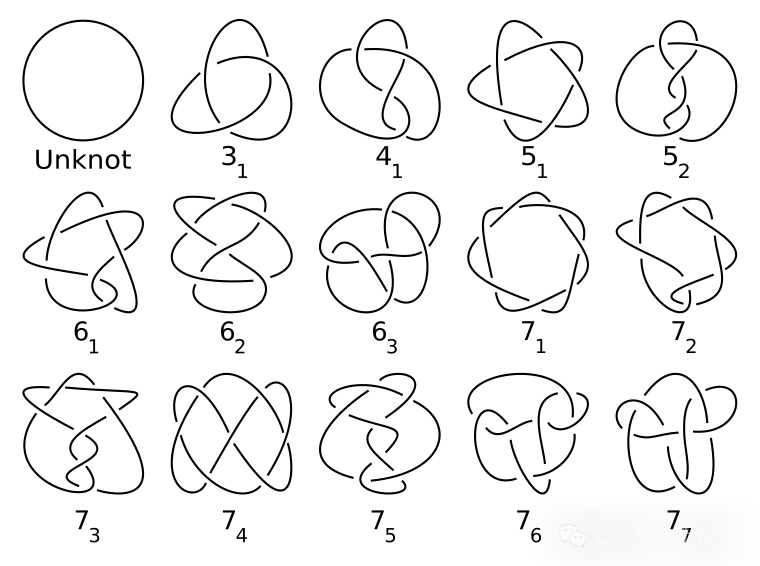
七个交叉点以内的素纽结(prime knots)
而在四维空间中,进阶版「莫比乌斯带」—— Klein瓶的演化更为生动。

如今,数学家们终于为这场关于维度奇异性的研究写下了尾声,而这项研究已经持续了65年。
几十年来,研究者们一直想弄清楚:究竟在哪些维度中,可能存在极其奇特的形状——
它们扭曲得如此极端,以至于无法通过所谓的标准拓扑操作「手术」(surgery)将其变换成一个普通球面。
研究表明,这类形状的存在,与拓扑学中的一个核心问题紧密相关:不同维度的球面之间到底存在怎样的联系?

末日猜想
上世纪50年代,数学家John Milnor震惊了整个数学界——他发现第七维空间中存在「异构球面」(exotic spheres)。

所谓异构球面,从拓扑学的角度看,它与普通球面是一样的——
即如果你只是关注形状在拉伸或扭曲下保持不变的特征,两者看不出区别。
但它们在「平滑性」上的定义却不一致:一个在普通球面上被认为是平滑的曲线,在异构球面上可能就不再平滑。
Milnor对这些异构球面产生了浓厚兴趣。
研究发现,在某些维度中这类球面非常罕见,而在另一些维度中,它们的数量可能多达几千个。
为此,Milnor引入了一种名为「手术」(surgery)的技术,这是一种受控地简化数学形状(即流形)并有可能将其转化为异构球面的方法。
这一方法后来成为研究流形的核心工具之一。
顾名思义,「手术」(surgery)是指将一个流形中某一部分切除,然后沿着切口的边界平滑地缝合上一个或多个新的部分。
缝合时必须保持「平滑」,不能出现尖角或边缘不连续的情况。
在处理扭曲形状的问题时,数学家还要求手术过程要保留流形的「框架」,即描述流形如何嵌入空间的一个技术性属性。
为了直观理解这一过程,让我们用一个例子来说明:
通过「手术」,可以将轮胎圈转化为篮球外皮,也就是把「环面」(torus)转化为「球面」。
一共分为4步:
1. 从轮胎圈中割下来一小圈;
2. 轮胎圈变成了空心意大利面;
3. 在轮胎圈两段缝上新补丁;
4. 缝好后,新「轮胎圈」在拓扑上等价于「球面」。

最终结果是一个普通的球面——事实上,在二维中并不存在异构球面。
但在某些更高的维度中,手术有时可以把流形转化为普通球面,有时则会转化为异构球面。
而在某些情况下,还存在第三种可能:某些流形根本无法通过手术转化为球面。
为了想象这种最后的情况,我们可以再次观察一个环面,只不过这次我们会对它做一些特殊的扭曲,以阻碍手术的进行:
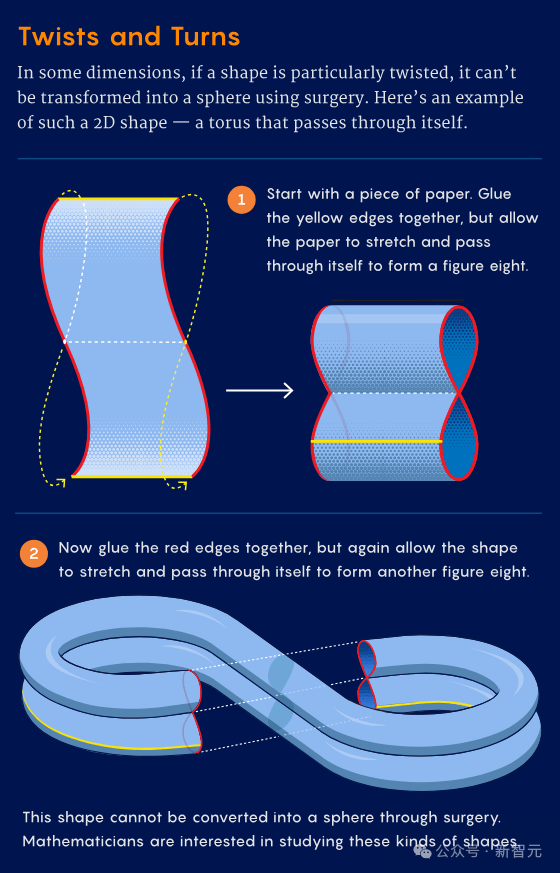
数学家们已经证明,无论如何操作,都无法通过手术将这个扭曲过的环面变成一个球面——不论是普通球面还是异构球面。这个流形属于完全不同的类别。
Kervaire不变量
1960年,法国数学家Michel Kervaire提出了一个不变量——称为Kervaire不变量。

每个光滑流形都有自己的Kervaire不变量:
如果一个流形可以通过手术变形成球面,那么它的Kervaire不变量为0;
如果不能,则为1。
如果一个流形可以通过手术变形成球面,那么它的Kervaire不变量为0;
如果不能,则为1。
因此,普通的环面的Kervaire不变量为0,而那个扭曲的环面则为1。
Kervaire借助这个不变量,开始探索不同维度中各种可能存在的流形。
他甚至构造出一个10维流形,其Kervaire不变量既不是0也不是1——
这意味着这个流形的结构扭曲得如此极端,以至于根本无法定义「平滑性」这种概念。
在此之前,没有人认为这样的流形可能存在。而随着这个强大不变量的出现,数学家们开始纷纷研究不同维度中流形的Kervaire不变量。
几年之内,研究者们已经证明,在维度2、6、14和30中确实存在Kervaire不变量为1的「扭曲流形」。
这些维度遵循一个规律:它们都是某个2的幂减2。
1969年,数学家William Browder证明了:只有这种形式的维度(即2^k-2)才有可能出现Kervaire不变量为1的流形。

于是,人们自然地假设:在所有这些维度中(如62、126、254等),应该都存在这类扭曲流形。
基于这个假设,有数学家构建了一整套关于异构球面与其他形状的猜想体系。
但问题是:这个假设有可能是错误的。
如果它被推翻,整个基于它建立的猜想体系也将随之崩塌。
这就是所谓的「末日猜想」(Doomsday Hypothesis)——它威胁着许多数学结构的稳定性与可信性。
悬而未解的尾巴
尽管数学家们在1984年证明了:在第62维中确实存在Kervaire不变量为1的扭曲流形,但此后在其他维度中的搜索却屡屡失败。
随着一次又一次的尝试无果,研究者逐渐失去了动力,这个问题也被边缘化,变成了数学研究中的一条「死胡同」。
2009年,为了「阻止这一课题被遗忘」,数学家Victor Snaith出版了一本书,探讨如果Browder列出的所有维度中都存在Kervaire不变量为1的流形,会带来哪些数学上的深远影响。

但在书的前言中,Snaith发出了一句预警:「这本书所讨论的内容,也许终将证明是并不存在的事物。」
然而,如果Snaith晚一年出版这本书,它的内容可能会完全不同。
就在书出版后的几周内,Michael Hill,Michael Hopkins和Doug Ravenel公布了一个令人震惊的结果:Snaith的警告是正确的。
他们证明,末日猜想是真的:
在第254维及更高维度中,不可能存在Kervaire不变量为1的流形。
这一结果让整个数学界陷入了一个奇特的局面:在所有无限可能的维度和流形形状中,只有一个维度仍然悬而未决,尚未被分类清楚。
那就是第126维。
用罗切斯特大学数学家Douglas Ravenel的话说:这是「一条悬而未解的尾巴」。

无尽的探索
数学家们早已知道:要解决某个维度上的Kervaire不变量问题,只需理解该维度对应的稳定同伦群。
问题在于,这正是拓扑学中最困难、最基础的问题之一。
如数学家Douglas Ravenel所说:「我不指望我的孙女辈的有生之年能看到它被完全解决。」
因此,数学家们只能逐步推进。
自1958年以来,他们一直在整理与稳定同伦群结构相关的信息,构建出一个庞大但尚未完成的「点图谱」——这就是著名的Adams谱序列(Adams spectral sequence)。
这个图谱用密密麻麻的点和线记录了关于稳定同伦群的复杂数据,是拓扑学中最重要的计算工具之一。
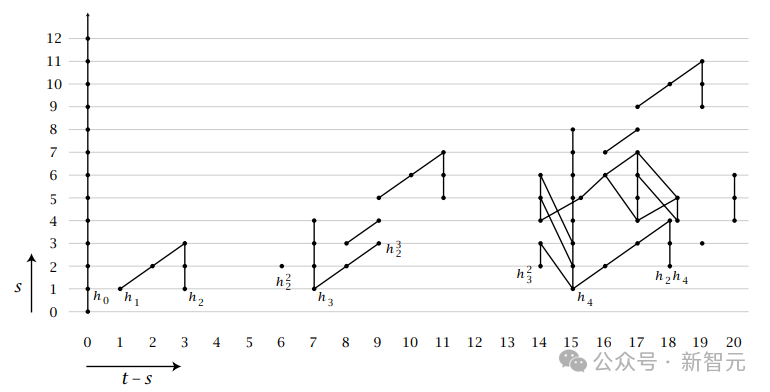
关于球面稳定同伦群的Adams谱序列E2页的可视化示意图
这本「图谱」最初的几页只是粗略的近似。
越靠后的页面,表示的就越接近真相。直到你翻到最后一页,也被称为「无穷页」(infinity page),那时所展现的就是对这些拓扑对象的完整准确描述。
这正是Adams谱序列的精髓:用一页页「望远镜式的检查」,在庞大的同伦世界中,逐步筛选出哪些结构是真实的、哪些只是幻象。
关键所在:126维
1969年,数学家William Browder证明了图谱第126列中一个特定点是解决该维度下Kervaire不变量问题的关键。
若该点能存活至无穷页,则126维流形必然存在两种类型:
半数具有Kervaire不变量零,半数具有Kervaire不变量1。
若该点消失,则126维流形仅存在Kervaire不变量零这一种类型。
对于第126列的特殊点,存在105种可能在抵达无穷页前消失的假设路径。
为了研究这些可能性,徐宙利与大学室友王国祯联手。

左:徐宙利;右:王国祯
在开发新计算技术的同时,他们将成果传递给徐宙利在研究生时期结识的数学家林伟南。
林伟南编写的程序成功排除了其中101种可能性。

随后经过一年攻坚,研究者们又开发出新方法排除了最后四种可能。
他们最终确认:Browder的特殊点确实能存活至无穷页——这意味着126维空间中存在具有Kervaire不变量1的流形。
在团队宣布结果之前,数学家们认为这样的计算遥不可及。
这项新工作「在计算上堪称壮举」。
其方法最终可能帮助数学家们进一步绘制巨大的Adams谱序列图谱。
前路漫漫,数学永无止境
新论文证明了维度126中存在奇异的扭曲形状,但并未提供如何构造它们的线索。
但在维度62和126中尚未找到任何这样的形状,尽管在这些维度中,这类形状占所有可能形状的整整一半。
尽管它们数量众多,Tillmann说:「我们实际上无法指出一个具体的例子。」
如果数学家们能够找出在维度62和126中构造扭曲形状的方法,可能会揭示这六个维度为何特殊的线索——
为什么只有在这六个维度中可以构建如此扭曲的形状。
Hopkins说:「通常当这种情况发生时,会有一些非常美丽的构造。」
这种构造「非常短暂,因为它只能在五六次中生效,而非无限多次。」
这项新工作「激励人们真正尝试找到这六个维度的特殊构造。」
Kervaire问题只是Adams谱序列中编码的一种维度异常。
特殊的Kervaire维度对应于图谱第二行中的六个特殊点。
最近,徐宙利和哥本哈根大学的Robert Burklund发现,少数特殊维度似乎在图谱第三行中展现出另一种奇特行为。

目前尚无人知晓这些维度中的特殊点对应于何种奇异流形,但数学家们希望能找到答案。
徐宙利表示,后续新的发现也很可能接踵而至。
「后面应该还有很多故事,等待我们去探索。」
2025-05-06 18:15 来源: 新智元
https://www.sohu.com/a/892506976_473283

















